Что такое динамическое программирование
Работу разработчика часто можно сравнить с решением головоломок. Как в настоящей головоломке, разработчику приходится тратить существенные ресурсы не столько на реализацию конкретного решения, сколько на выбор оптимального подхода. Иногда задача решается легко и эффективно, а порой — только полным перебором всех возможных вариантов. Такой подход часто называют наивным решением. Он имеет существенный минус — временные затраты.
Представим хакера, который пытается взломать какой-то пароль перебором всех комбинаций символов. Если пароль допускает 10 цифр, 26 маленьких букв, 26 больших букв и 32 специальных символа (например, значок доллара), то для каждого символа в пароле есть 94 кандидата. Значит, чтобы взломать перебором пароль, состоящий из одного символа, потребуется 94 проверки. Если в пароле два символа — 94 кандидата на первую позицию, 94 кандидата на вторую позицию — то придется перебрать аж 94*94 = 8836 возможных пар. Для пароля из десяти символов потребуется уже перебор 94^10 комбинаций.
Если обобщить, то для взлома пароля с произвольной длиной N требуется O(94^N) операций. Такие затраты часто называют «экспоненциальными»: появление каждой новой позиции влечёт за собой увеличение количества операций в 94 раза. Взлом пароля может показаться чем-то экзотическим, но задачи, требующие полного перебора всех вариантов — совсем не экзотика, скорее угрюмая реальность.
Экспоненциальное время — это долго. Даже O(2^N) — это просто непозволительно долго. Настолько долго, что никому и в голову не придет запустить подобный алгоритм даже на простых данных — ведь на решение такой задачи с сотней элементов потребуются тысячи, миллионы или миллиарды лет вычислений. А в реальной жизни нужно решать задачи с намного большим количеством элементов. Как же быть?
Дело в том, что многие задачи без эффективного алгоритма решения можно решить за привлекательное время с помощью одной хитрости — динамического программирования.
Динамическое программирование
Динамическое программирование — это особый подход к решению задач. Не существует какого-то единого определения динамическому программированию, но все-таки попробуем её сформировать. Идея заключается в том, что оптимальное решение зачастую можно найти, рассмотрев все возможные пути решения задачи, и выбрать среди них лучшее.
Работа динамического программирования очень похожа на рекурсию с запоминанием промежуточных решений — такую рекурсию еще называют мемоизацией. Рекурсивные алгоритмы, как правило, разбивают большую задачу на более мелкие подзадачи и решают их. Динамические алгоритмы делят задачу на кусочки и вычисляют их по очереди, шаг за шагом наращивая решения. Поэтому динамические алгоритмы можно представить как рекурсию, работающую снизу вверх.
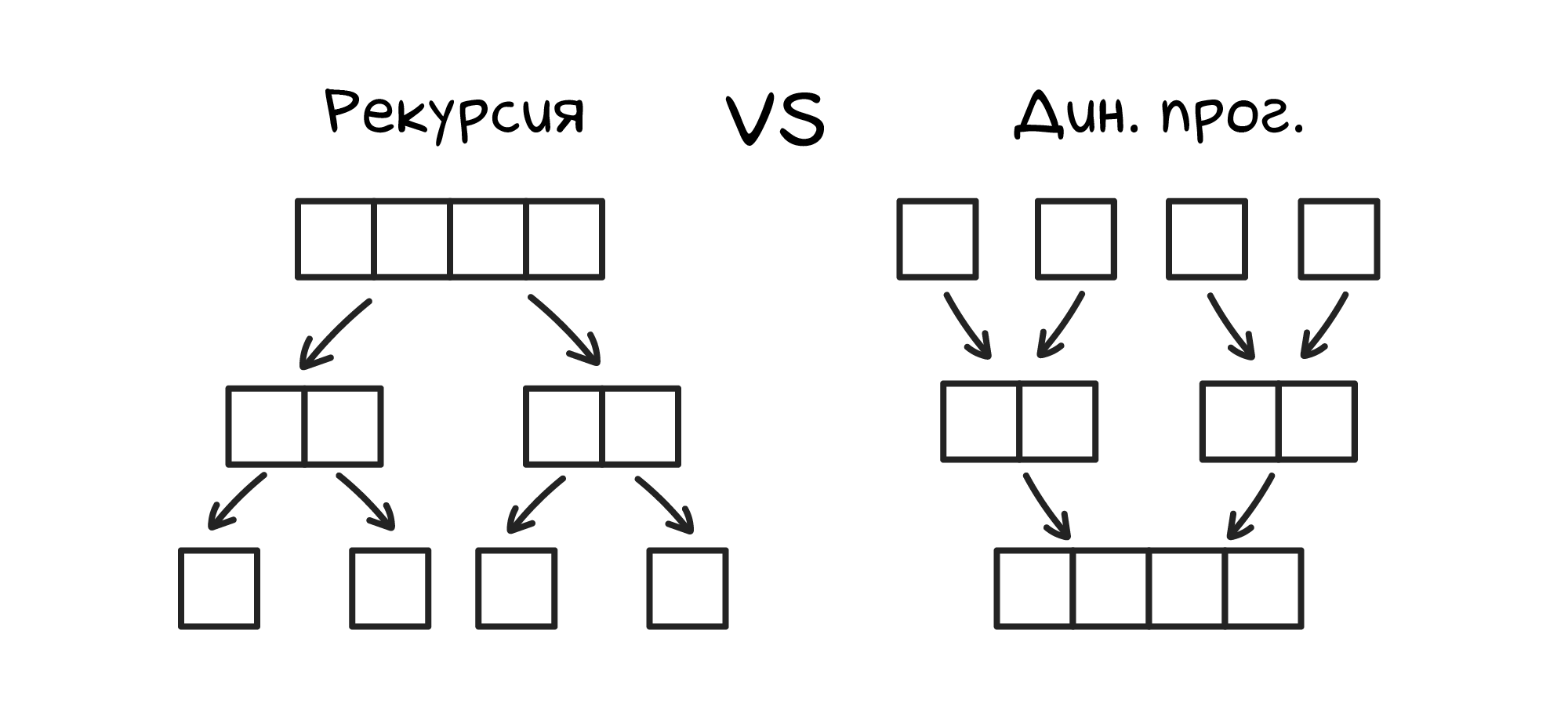
Магия динамического программирования заключается в умном обращении с решениями подзадач. «Умный» в этом контексте значит «не решающий одну и ту же подзадачу дважды». Для этого решения мелких подзадач должны где-то сохраняться. Для многих реальных алгоритмов динамического программирования этой структурой данных является таблица.
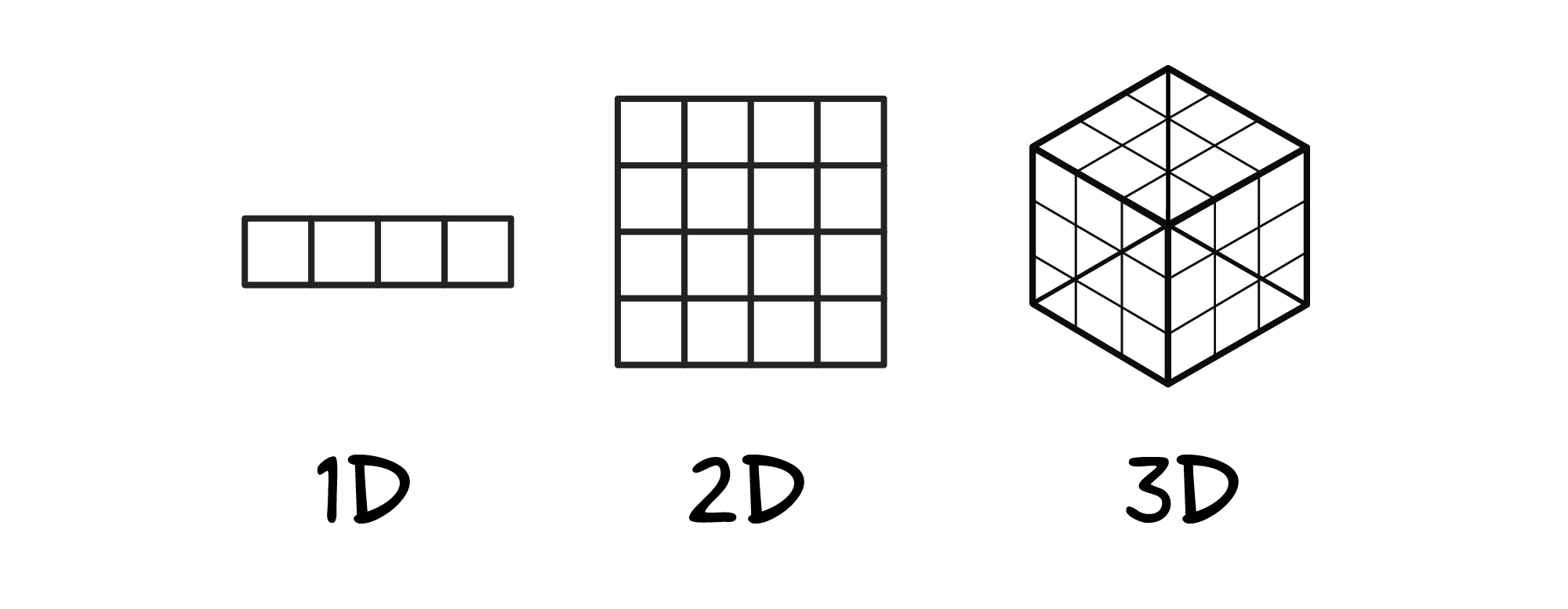
В самых простых случаях эта таблица будет состоять только из одной строки — аналогично обычному массиву. Эти случаи будут называться одномерным динамическим программированием, и потреблять O(n) памяти. Например, алгоритм эффективного вычисления чисел Фибоначчи использует обычный массив для запоминания вычисленных промежуточных результатов. Классический рекурсивный алгоритм делает очень много бессмысленный работы — он по миллионному разу рассчитывает то, что уже было рассчитано в соседних ветках рекурсии.
В самых распространённых случаях эта таблица будет выглядеть привычно и состоять из строчек и столбиков. Обычная таблица, похожая на таблицы из Excel. Это называется двумерным динамическим программированием, которое при n строках и n столбцах таблицы потребляет O(n*n) = O(n^2) памяти. Например, квадратная таблица из 10 строк и 10 столбцов будет содержать 100 ячеек. Чуть ниже будет подробно разобрана именно такая задача.
Бывают и более запутанные задачи, использующие для решения трехмерные таблицы, но это редкость — решение задачи с использованием трехмерной таблицы зачастую просто нельзя себе позволить. Небольшая двухмерная таблица на 1024 строки и 1024 столбца может потребовать несколько мегабайт памяти. Трехмерная таблица с такими же параметрами будет занимать уже несколько гигабайт.
Что нужно, чтобы решить задачу динамически, помимо ее исходных данных? Всего три вещи:
- Таблица, в которую будут вноситься промежуточные результаты. Один из них будет выбран в конце работы алгоритма в качестве ответа
- Несколько простых правил по заполнению пустых ячеек таблицы, основанных на значениях в уже заполненных ячейках. Универсального рецепта тут нет и к каждой задаче требуется свой подход
- Правило выбора финального решения после заполнения таблицы
Разберем эти принципы на примере.
Пример решения задачи
Демонстрационным подопытным выступит классическая задача динамического программирования — Расстояние Левенштейна. Несмотря на кажущееся сложным название, в действительности это задача о трансформации одного слова в другое путем добавления, удаления и замены букв с минимальным количеством операций.
Эта задача может быть сформулирована так: найти минимальное «расстояние» между двумя словами. Расстоянием в этом случае будет минимальное количество операций, которые нужно применить к первому слову, чтобы получить второе (или наоборот).
Доступных операции у нас три:
- insert — добавить одну букву в любое место в слове, в том числе в самое начало и в конец
- delete — удалить одну букву из любого места в слове
- replace — заменить одну букву в определенном месте на другую букву
Все эти операции имеют равную стоимость: +1 к расстоянию между словами.
Возьмем для примера два простых слова, MONEY и MONKEY. Какое минимальное количество операций необходимо, чтобы превратить MONEY в MONKEY? Находчивый человеческий глаз быстро смекнет, что одна: добавить букву K после между третьей и четвертой буквой.
Возьмем случай посложнее. Попробуем превратить слово SUNDAY в слово SATURDAY, и увидим, что количество комбинаций, которые нужно перебрать, потенциально очень велико. Если решать задачу перебором, то можно рассмотреть все возможные комбинации, как в примере со взломом пароля. Вместо возможных 94 символов-кандидатов у нас есть три операции — insert, delete, replace. Три комбинации для первой буквы, 3*3 для двух букв, 3*3*3 для трех букв, 3^N для N букв. Комбинаторный взрыв.
Динамическое решение
Приступим к динамическому решению. Для начала, создадим таблицу и разместим исходные слова на ее краях, оставив немного свободного места. Второй столбик и вторую строчку буем использовать для пустых строк — их часто обозначают символом ε, читается epsilon. Аналог того, что вы имеете в виду, когда используете пустую строку на своем языке программирования: String eps = “”.
| ε | S | A | T | U | R | D | A | Y | |
|---|---|---|---|---|---|---|---|---|---|
| ε | |||||||||
| S | |||||||||
| U | |||||||||
| N | |||||||||
| D | |||||||||
| A | |||||||||
| Y |
Теперь заполним второй столбик и вторую строчку, руководствуясь абсолютно интуитивными соображениями: как превратить пустую строку в какую-то строку? Конечно же, добавить в нее нужные символы! Например, чтобы перевести ε в SATU, необходимо добавить букву S, букву A, букву T и букву U. Четыре операции. Что делать с превращением ε в ε (вторая строка, второй столбец)? Элементарно — ничего делать не нужно, ноль действий.
| ε | S | A | T | U | R | D | A | Y | |
|---|---|---|---|---|---|---|---|---|---|
| ε | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| S | 1 | ||||||||
| U | 2 | ||||||||
| N | 3 | ||||||||
| D | 4 | ||||||||
| A | 5 | ||||||||
| Y | 6 |
Теперь нужна система простых правил, с помощью которой мы сможем заполнить таблицу. Таблица будет именоваться D, а первая строчка и столбик останутся на ее полях. Работать с таблицей мы будем, как с двухмерным массивом: D[0, 2] означают ячейку на пересечении нулевой строки и второго столбика. В нашем примере D[0, 2] = 2.
Также назовём слово по вертикали A, а слово по горизонтали B. Эта парочка нам нужна, чтобы иметь доступ к оригинальным словам на полях. Из-за дополнительных колонок в для ε индексы в A и B отличаются от индексов в таблице. Если быть точнее — они сдвинуты на единицу. A[0] = S, A[1] = U, A[2] = N, B[7] = Y, и так далее.
Наконец, создадим наше правило заполнения таблицы. Для каждой новой ячейки мы проверяем верхнюю, левую или лево верхнюю по диагонали соседние ячейки. Из трех чисел будет выбрано наименьшее и записано в новую ячейку.
D[i, j] = minimum(
D[i-1, j] + 1, // delete
D[i, j-1] + 1, // insert
D[i-1, j-1] + (A[i-1] == B[j-1] ? 0 : 1) // replace
)
Это важный момент в динамическом программировании: правила кажутся бессмысленными, а собрать общую картину происходящего в голове сложно. Давайте посмотрим на маленький кусочек таблицы — возможно, он прольет свет на некоторые детали.
| ε | S | A | |
|---|---|---|---|
| ε | 0 | 1 | 2 |
| S | 1 | ||
| U | 2 |
Что следует записать в ячейку D[1,1] как результат перехода из S в S? Интуитивно ясно, что для этого ничего делать и не нужно, ноль операций. Запишем в ячейку ноль. На что похоже это значение, учитывая, что вычитать ничего нельзя? Среди соседей ноль есть только по диагонали.
| ε | S | A | |
|---|---|---|---|
| ε | 0 | 1 | 2 |
| S | 1 | 0 | |
| U | 2 |
Что записать в ячейку D[2,1] как результат перехода из SU в S? Нужно удалить букву U — значит, это одна операция. По-сути, стоимость перехода из SU в S будет равно стоимости удаления буквы U и перехода из S в S (чья стоимость уже была посчитана и лежит в ячейке D[1,1]).
| ε | S | A | |
|---|---|---|---|
| ε | 0 | 1 | 2 |
| S | 1 | 0 | |
| U | 2 | 1 |
Теперь посмотрим на ячейку D[1,2], переход из S в SA. Да, именно, стоимость перехода будет равна стоимости добавления буквы A и перехода из S в S, итого единица.
| ε | S | A | |
|---|---|---|---|
| ε | 0 | 1 | 2 |
| S | 1 | 0 | 1 |
| U | 2 | 1 |
Последняя ячейка, D[2,2], переход из SU в SA. Самым оптимальным решением было бы заменить букву U на букву A, плюс цена бесплатного перехода из S в S.
| ε | S | A | |
|---|---|---|---|
| ε | 0 | 1 | 2 |
| S | 1 | 0 | 1 |
| U | 2 | 1 | 1 |
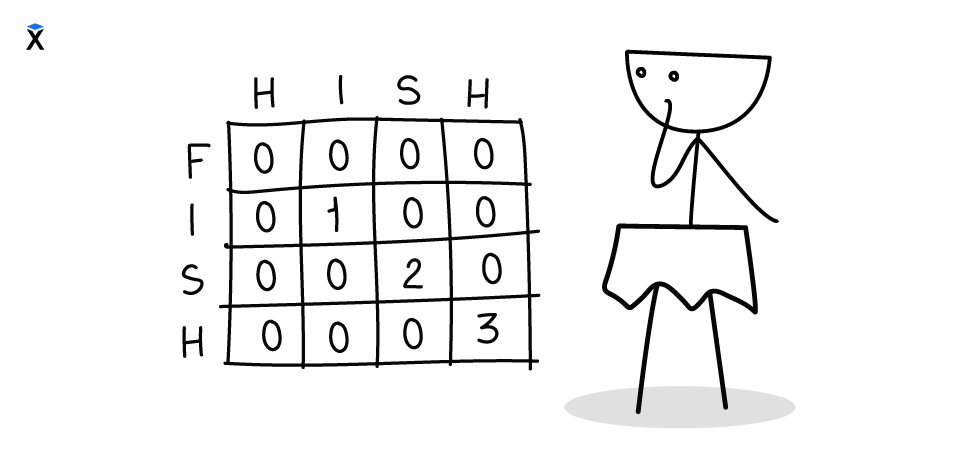
В самой правой нижней ячейке содержится финальная стоимость перехода из слова SU в слово SA. Аналогичным образом можно заполнить всю таблицу. Из ячейки D[6,8] мы узнали, что переход из слова SUNDAY в слово SATURDAY стоит минимум три операции. Жирным шрифтом выделим оптимальный путь.
Давайте проследим его по шагам. Переход из S в S ничего не стоит. Переход из S в SA стоит одну операцию. Переход из S в SAT стоит две операции. Переход из SU в SATU стоит две операции. Переход из SUN в SATUR стоит три операции. Переход из SUND в SATURD стоит три операции (стоимость предыдущего перехода плюс нулевая цена перехода из D в D). Переход из SUNDA в SATURDA стоит три операции. Наконец, переход из SUNDAY в SATURDAY требует тех же трёх операций.
Кстати, если присмотреться к таблице, можно заметить, что оптимальных решений несколько: из D[1,2] можно перейти как в D[1,3], так и в D[2,2]. В этой постановке задачи нас интересует только минимальное количество, а не список всех возможных путей решения, так что это не существенно.
| ε | S | A | T | U | R | D | A | Y | |
|---|---|---|---|---|---|---|---|---|---|
| ε | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| S | 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U | 2 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 6 |
| N | 3 | 2 | 2 | 2 | 3 | 3 | 4 | 5 | 6 |
| D | 4 | 3 | 3 | 3 | 3 | 4 | 3 | 4 | 5 |
| A | 5 | 4 | 3 | 4 | 4 | 4 | 4 | 3 | 4 |
| Y | 6 | 5 | 4 | 4 | 5 | 5 | 5 | 4 | 3 |
Вот так, собственно, и выглядит большинство решений из мира динамического программирования. Кстати, это решение имеет название — алгоритм Вагнера-Фишера. Забавный факт: этот алгоритм практически параллельно опубликовали разные группы незнакомых ученых с разных концов планеты в эпоху, когда еще не был интернета. Товарищи Вагнер и Фишер, кстати, были далеко не первыми.
Давайте теперь рассмотрим, в чем отличия применения этого алгоритма от решения перебором.
Анализ решения
Как уже было сказано, решение перебором этой задачи простой рекурсией имеет временную сложность O(3^n), но не требует лишней памяти — значит, O(1) операций в памяти.
Какие издержки у динамического решения? Давайте представим, что сравниваются слова равной длины, по n символов в слове. Все решение сводится к заполнению таблицы с n+1 строчками (отдельная для пустой строки ε), и n+1 столбиками. Значит, используется (n+1)^2 ячеек. Не будем считать копейки, и округлим количество ячеек до n^2. Для каждой ячейки мы будем проверять трех ее соседей, что требует константного времени O(1). Значит, на заполнение всей таблицы потребуется O(n^2) операций.
Какой будет расход памяти? Для таблицы с n^2 ячеек нам нужно O(n^2) памяти.
Если слова разной длины, то можно либо смотреть по самому длинному, либо несколько повысить степень сложности формулы. Например, если первое слово имеет длину n, а второе — m, то потребуется O(nm) времени и O(nm) памяти.
Итог
Основная идея динамического программирования должна прослеживаться в представленном примере: мы жертвуем солидным количеством памяти (O(nm) вместо O(1)), но получаем просто сумасшедший выигрыш во времени (O(nm) против O(3^n)).
Перечислим все ключевые особенности динамического программирования.
Преимущества:
-
Скорость. Главное достоинство динамического программирования. Нерешаемые задачи становятся решаемыми, в большинстве случаев — за квадратичное время! Одна операция на заполнение каждой ячейки таблицы — и вопрос закрыт.
-
Универсальность. One Ring to rule them all — создание компактной системы из нескольких правил для заполнения таблицы гарантирует решение задачи на любых данных. Ни исключений, ни пограничных случаев, несколько строчек, — и сложная проблема решена.
-
Точность. Поскольку алгоритм динамического программирования рассматривает абсолютно все возможные варианты и сценарии, он гарантированно обнаружит самое оптимальное решение. Никакой потери точности, никаких приблизительных ответов. Если решение существует — оно будет найдено.
Недостатки:
-
Память. В большинстве случаев алгоритмы динамического программирования требуют времени на построение и заполнение таблиц. Таблицы потребляют память. Это может стать проблемой: в случае, если сами таблицы очень большие, или если для решения какой-то задачи нужно построить очень много таких таблиц и держать их всех в памяти.
-
Когнитивная нагрузка. Решение запутанной задачи с помощью компактной системы правил — очень заманчивая идея. Но тут есть один нюанс: для составления или хотя бы для понимания этих систем правил необходимо научиться «думать на динамическом программировании». Это является причиной довольно спорной репутации динамического программирования.
Области применения
Динамическое программирование — не теоретическая конструкция, которая не выходит за рамки научных работ. Оно пользуется популярностью во многих прикладных областях. Их достаточно много: прикладная математика, машиностроение, теории управления или прогнозирование финансовых данных. Но мы остановимся на одной — на биоинформатике.
Ученые в этой области занимаются «оцифровыванием» биологического материала, а так же хранением и анализом полученной информации. В этой науке сотни захватывающих аспектов, и она ставит перед разработчиками очень серьезные задачи, ведь данных невероятно много. Например, в геноме человека около трех миллиардов пар нуклеотидов (кирпичиков ДНК). Одна пара обычно кодируется одним байтом, в итоге выходит около трех миллиардов байт информации на один-единственный геном — три гигабайта данных на одного человека.
Один геном не создает серьезных проблем, но геномы сами по себе малоинтересны: чтобы обнаружить мутации в геноме конкретного человека, нужно сначала «выровнять» его с другими, референсными геномами (выровненными и размеченными заранее). Возможных вариантов этого выравнивания может быть огромное количество, но нужно найти самый правдоподобный из них. То есть вариант, у которого максимальная вероятность возникновения. Например, вариант с наименьшим количеством мутаций. Если принять во внимание, что генетический код обычно хранятся в виде очень длинных строк, состоящих из разных букв, то пример с Расстоянием Левенштейна начинает играть новыми красками. Эта задача, потенциально приводящая к комбинаторному взрыву (прямо как перебор всех комбинаций символов для взлома пароля), замечательно решается методами динамического программирования!
Если интересно, почитайте про Multiple Sequence Alignment (MSA)
Это только один пример. Биоинформатика буквально живет динамическим программированием — вот еще несколько примеров:
- Построение молекулярных деревьев для определения последовательности эволюционных изменений
- Эффективный перевод генетической информации (например, из кусочка кожи) в длинную строку в базе данных
Если 15 лет назад полное считывание генома (секвенирование) имело себестоимость в десятки миллионов долларов, то сегодня эта услуга стоит одну-две тысячи долларов, и постепенно дешевеет. Этот скачок произошел не столько за счет роста вычислительных мощностей, сколько за счет появления эффективных алгоритмов.